Congruence

More Specific Topics in Congruence

Popular Tutorials in Congruence

How Do You Use Matrices to Translate a Figure?

Matrices can help you solve all sorts of problems! In this tutorial, you'll see how to use a translation matrix to translate a figure on the coordinate plane.
How Do You Bisect a Segment by Constructing?
How Do You Construct a Line Parallel to Another Line Through a Given Point?

A compass is a very handy tool! In this tutorial, you'll see how to use a compass and straightedge to construct parallel lines!
What is the Corresponding Angles Postulate?

When a transversal intersects parallel lines, the corresponding angles created have a special relationship. The corresponding angles postulate looks at that relationship! Follow along with this tutorial to learn about this postulate.
What is the Converse of the Corresponding Angles Postulate?

The corresponding angles postulate states that when a transversal intersects parallel lines, the corresponding angles are congruent. What if you go the other way and start with corresponding angles that are congruent? Is the converse of this postulate true? This tutorial explores exactly that!
How Do You Determine if Triangles on the Coordinate Plane are Congruent?

There are many ways to show that two triangles are congruent. This tutorial shows you how to use a triangle congruence postulate to show that two triangles on the coordinate plane are congruent to each other!
How Do You Use a Congruence Postulate to Prove Triangles are Congruent?

When proving two triangles are congruent, you use information and postulates you already know to create a logical trail from what you know to what you want to show. This tutorial shows an example of using a congruence postulate to show two triangles are congruent!
How Do You Show that Corresponding Parts of Congruent Triangles are Congruent?

If you're given information about two triangles and asked to prove parts of the triangles are congruent, see if you can show the two triangles are congruent. If they are, then you know that the corresponding parts are congruent! Follow along with this tutorial to see an example.
How Do You Prove that Two Overlapping Triangles are Congruent?

Proofs are an important part of geometry. This tutorial shows you how to use given information to prove that two overlapping triangles are congruent!
How Do You Identify Common Parts in Overlapping Triangles?

It might seem like a challenge to make sense of figures with overlapping triangles, but it's not so difficult! This video gives some commonsense advice for identifying common angles and common sides in these figures.
How Do You Construct an Equilateral Triangle?

This tutorial shows you how to construct an equilateral triangle using a ruler and compass.
What is the Side-Angle-Side Postulate for Triangle Congruence?

The Side-Angle-Side postulate is just one of many postulates you can use to show two triangles are congruent. This tutorial introduces you to the SAS postulate and shows you how to use it!
What is the Angle-Side-Angle Postulate for Triangle Congruence?

What is the Angle-Side-Angle postulate? This postulate is just one of many postulates you can use to prove two triangles are congruent! This tutorial explains the ASA postulate.
What is CPCTC?

The term CPCTC can come up a lot when you're dealing with congruent triangles, but what does it mean? This tutorial gives a great explanation and shows you how to use it in an example!
What is the Hypotenuse-Leg Congruence Theorem?

There's a special theorem that helps you quickly figure out if two right triangles are congruent. This tutorial introduces you to that theorem and shows you how to use it!
How Can You Tell if a Point is on the Perpendicular Bisector of a Line Segment?

If you want to determine if a point is on the perpendicular bisector of a line segment, the Perpendicular Bisector Theorem and its converse might come in handy. This tutorial gives a great example of how to tell if a given point is a perpendicular bisector of a segment!
How Do You Use the Centroid to Find Segment Lengths in a Triangle?

When you're given the centroid of a triangle and a few measurements of that triangle, you can use that information to find missing measurements in the triangle! This tutorial shows you how it's done.
How Do You Use the Hinge Theorem to Compare Side Lengths in Two Triangles?

The Hinge Theorem helps you compare side measurements of two triangles when you have two sets of congruent sides. Follow along with this tutorial to see this theorem used to find the relationship between the sides of two triangles.
How Do You Construct a Perpendicular Bisector?

This tutorial shows you how to construct a perpendicular bisector using only a compass and a straightedge!
How Do You Write an Indirect Proof?

This tutorial looks at using an indirect proof to show that an equilateral triangle cannot have a right angle.
How Do You Put the Sides of a Triangle in Order According to Size if You Know Two Angles of the Triangle?

Trying to figure out which side of a trianlge is the shortest? How about the longest? All you need to get your answer are the angle measurements of the triangle! How does it work? Watch this tutorial to find out!
What is the Circumcenter of a Triangle?

This tutorial explains the ins and outs of the circumcenter of a triangle. You'll see how to build up from the Perpendicular Bisector Theorem to find the circumcenter of a triangle.
What is the Incenter of a Triangle?

The incenter of a triangle deals with the angle bisectors of a triangle. This tutorial shows you how to find the incenter of a triangle by first finding the angle bisectors.
What is the Hinge Theorem?

What's the Hinge Theorem all about? Watch this tutorial to find out!
What is a Perpendicular Bisector?

Looking at the term 'perpendicular bisector', you can bet it has something to do with perpendicular lines! This tutorial talks all about perpendicular bisectors and shows you exactly what the term means.
What is the Triangle Midsegment Theorem?

The triangle midsegment theorem looks at the relationship between a midsegment of a triangle and the triangle's third side. Follow along with this tutorial to learn about the triangle midsegment theorem.
What is a Median of a Triangle?

A median of a triangle is a special line segment that connects two pieces of a triangle. This tutorial introduces you to the median of a triangle and shows you how many medians each triangle has!
How Do You Find Values for Variables in the Angles of a Quadrilateral To Make it a Parallelogram?

When you're given a quadrilateral with some of the interior angles defined with variables, you can find what values those variables need to have to make that quadrilateral a parallelogram. Follow along with this tutorial to learn what steps to take to get the answer!
How Do You Use the Diagonals of a Rectangle to Find the Value of a Variable?

When you make diagonals inside a rectangle, those diagonals are congruent. With this information, you can find the value of a variable that's part of a measurement of a diagonal. This tutorial shows you the steps.
How Do You Find the Value for a Variable in the Angles of a Quadrilateral To Make it a Rhombus?

A parallelogram needs to have certain qualities in order to be a rhombus. In this tutorial, you'll use your knowledge of these shapes in order to find the value for a variable that will make a given parallelogram a rhombus.
How Do You Construct a Square?

Did you know you don't need a ruler to construct a square? All you need is a compass and a straightedge! Watch this tutorial to see how it's done!
How Do You Graph a Glide Reflection?

When you graph a composition of two transformations, you have to be very careful to perform all the steps in the right order! Watch this tutorial to see how to graph a glide reflection.
How Do You Identify a Congruence Transformation?

Want to figure out whether two figures are congruent? There's a mathematically precise way to do this! Watch this tutorial on congruence transformations to learn more.
What is a Congruence Transformation, or Isometry?

Not all transformations are created equal! Congruence transformations, or isometries, have a special property that distinguishes them from other transformations. This tutorial will show you what makes them special!
What is a Dilation?

When someone's eyes dilate, their pupils get bigger or smaller, but they always stay the same shape. Dilation in math is very similar. When you dilate a figure, you change the size of the figure without changing its shape. This tutorial introduces you to dilation. Take a look!
How Do You Use a Graph to Reflect a Figure Over the Y-Axis?

Reflecting a figure over the y-axis can be a little tricky, unless you have a plan. In this tutorial, see how to use the graph of a figure to perform the reflection. Check it out!
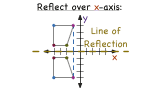
How Do You Use Coordinates to Reflect a Figure Over the X-Axis?

Want to see how to reflect a figure over the x-axis? Then this tutorial was made for you! In this tutorial, you'll see how to use coordinates from the original figure to reflect the figure over the x-axis. Take a look!
How Do You Use Coordinates to Reflect a Figure Over the Y-Axis?

Want to see how to reflect a figure over the y-axis? Then this tutorial was made for you! In this tutorial, you'll see how to use coordinates from the original figure to reflect the figure over the y-axis. Take a look!
How Do You Use a Graph to Reflect a Figure Over the X-Axis?

Reflecting a figure over the x-axis can be a little tricky, unless you have a plan. In this tutorial, see how to use the graph of a figure to perform the reflection. Check it out!
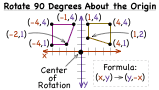
How Do You Rotate a Figure 90 Degrees Around the Origin?

Rotating a figure about the origin can be a little tricky, but this tutorial can help! This tutorial shows you how to rotate coordinates from the original figure about the origin. Then, simply connect the points to create the new figure. See this process in action by watching this tutorial!
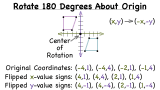
How Do You Rotate a Figure 180 Degrees Around the Origin?

Rotating a figure about the origin can be a little tricky, but this tutorial can help! This tutorial shows you how to rotate coordinates from the original figure about the origin. Then, simply connect the points to create the new figure. See this process in action by watching this tutorial!
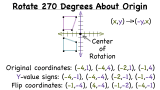
How Do You Rotate a Figure 270 Degrees Clockwise Around the Origin?

Rotating a figure about the origin can be a little tricky, but this tutorial can help! This tutorial shows you how to rotate coordinates from the original figure about the origin. Then, simply connect the points to create the new figure. See this process in action by watching this tutorial!
How Do You Use a Graph to Translate a Figure Horizontally?

Translating a figure on the coordinate plane is easier than you might think! In this tutorial, see how to use the graph of the original figure to perform the translation. Take a look!
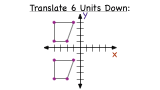
How Do You Use a Graph to Translate a Figure Vertically?

Translating a figure on the coordinate plane is easier than you might think! In this tutorial, see how to use the graph of the original figure to perform the translation. Take a look!
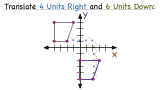
How Do You Use a Graph to Translate a Figure Diagonally?

Performing multiple translations on the graph of a figure is easier than you might think! In this tutorial, see how to use the graph of the original figure to perform each translation in order to get the graph of the new figure. Check it out!
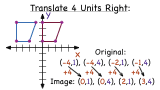
How Do You Use Coordinates to Translate a Figure Horizontally?

Translating a figure on the coordinate plane is easier than you might think! This tutorial shows you how to translate coordinates from the original figure. Then, simply connect the points to create your new figure. This tutorial shows you how!
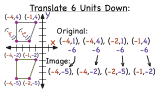
How Do You Use Coordinates to Translate a Figure Vertically?

Translating a figure on the coordinate plane is easier than you might think! This tutorial shows you how to translate coordinates from the original figure. Then, simply connect the points to create your new figure. This tutorial shows you how!
What is a Parallelogram?

A parallelogram is a special type of quadrilateral with some special properties. In this tutorial, take a look at parallelograms and learn what kinds of quadrilaterals can also be called parallelograms!
What is a Point?

A point is a fundamental building block of math. Without points, you couldn't make lines, planes, angles, or polygons. That also means that graphing would be impossible. Needless to say, learning about points is very important! That makes this tutorial a must see!
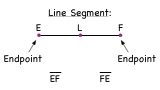
What is a Line Segment?

A math term can really tell you a lot about the thing it's describing. Take the term line segment. A line segment is just part of a line! In this tutorial, learn about line segments, how to name them, and what the midpoint of a line segment is!
What is an Angle?

Angles are a fundamental building block for creating all sorts of shapes! In this tutorial, learn about how an angle is formed, how to name an angle, and how an angle is measured. Take a look!
What are Vertical Angles?

Vertical angles have a very special quality. They are always congruent to one another! Check out this tutorial to learn about and see how to identify vertical angles!
What are Parallel Lines?

Lines that are parallel have a very special quality. Without this quality, these lines are not parallel. In this tutorial, take a look at parallel lines and see how they are different from any other kind of lines!
What are Perpendicular Lines?

Perpendicular lines have a special property. The angles formed by perpendicular lines will always be the same. Check out this tutorial to learn about perpendicular lines and see a cool trick involving these special lines!
What is a Transversal?

Ever heard of a transversal? It's not as confusing as the term sounds. This tutorial will introduce you to transversals and show you the neat things that happen when a transversal meets two parallel lines. Take a look!
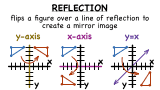
What is a Reflection?

When you look in the mirror, you see your reflection. In math, you can create mirror images of figures by reflecting them over a given line. This tutorial introduces you to reflections and shows you some examples of reflections. Take a look!
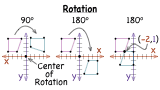
What is a Rotation?

Ever turned a door handle? You were performing a rotation! In math, rotations are just the same! Check out this tutorial to learn about rotations.
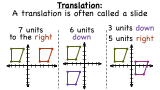
What is a Translation?

Ever slide something across a table? If so, then you have performed a translation! In this tutorial, learn the definition of translation and see some really neat examples. Take a look!
What is a Transformation?

Transformations can be really fun! They allow you to change or move a figure. In this tutorial, learn about all the different kinds of transformations!
What is an Image?

Just about everything in math has a name! Did you know that when you're dealing with transformations, the new figure you get is called an image? Check out this tutorial and learn about this math term!
What is the Triangle Sum Theorem?

When you're dealing with triangles, the Triangle Sum theorem can be very useful in finding interior angle measurements. In this tutorial, learn how to find this helpful theorem!
What is a Circle?

Circles are a fundamental part of math! In this tutorial, you'll be introduced to circles and see the different parts of a circle such as the diameter, radius, and chord. Check out this tutorial to learn about circles!