Transformational Geometry

More Specific Topics in Transformational Geometry

Popular Tutorials in Transformational Geometry

How Do You Identify Transformations in the Equation of a Rational Function?

If you can figure out how the equation of a rational function was transformed, then you can make a good sketch of that function without finding lots of individual points. Take a look at the video to learn more!
What is the Parent Function for a Rational Function?

Like linear, quadratic, and cubic functions, rational functions also have a parent. It's also the parent function for the reciprocal function family. Check out this tutorial to learn more about its characteristics!
How Do You Graph a Rational Function by Finding its Asymptotes and Zeros?

In a rational function, the denominator of the rational expression holds the key to the location of the vertical asymptotes. The relationship between degrees of the numerator and denominator determine the nature of the horizontal asymptotes. Check out the tutorial to learn more!
How Do You Use the Equation for a Rational Function to Find Its Horizontal Asymptotes?

Rational functions behave predictably as they head off to infinity. Follow this tutorial to learn more about their asymptotic behavior!
How Do You Graph a Glide Reflection?

When you graph a composition of two transformations, you have to be very careful to perform all the steps in the right order! Watch this tutorial to see how to graph a glide reflection.
How Do You Identify a Congruence Transformation?

Want to figure out whether two figures are congruent? There's a mathematically precise way to do this! Watch this tutorial on congruence transformations to learn more.
How Do You Graph a Translation Then a Dilation?

When you graph a composition of two transformations, you have to be very careful to perform all the steps in the right order! Watch this tutorial to see how to graph a translation of a figure, followed by a dilation.
What is a Congruence Transformation, or Isometry?

Not all transformations are created equal! Congruence transformations, or isometries, have a special property that distinguishes them from other transformations. This tutorial will show you what makes them special!
What Makes Two Figures Congruent?

When are two figures congruent? When you can move one on top of the other without changing its size or shape! Check out this tutorial to learn more about using isometries to map congruent figures onto each other.
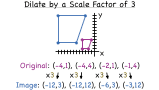
How Do You Make a Figure Larger Using a Dilation?

Dilation allows you to shrink or enlarge the size of a figure without changing its shape. In this tutorial, follow along as you see how dilate a figure by a given scale factor. Check it out!
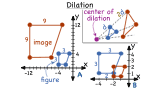
What is a Dilation?

When someone's eyes dilate, their pupils get bigger or smaller, but they always stay the same shape. Dilation in math is very similar. When you dilate a figure, you change the size of the figure without changing its shape. This tutorial introduces you to dilation. Take a look!
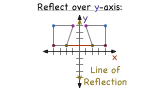
How Do You Use a Graph to Reflect a Figure Over the Y-Axis?

Reflecting a figure over the y-axis can be a little tricky, unless you have a plan. In this tutorial, see how to use the graph of a figure to perform the reflection. Check it out!
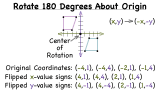
How Do You Rotate a Figure 180 Degrees Around the Origin?

Rotating a figure about the origin can be a little tricky, but this tutorial can help! This tutorial shows you how to rotate coordinates from the original figure about the origin. Then, simply connect the points to create the new figure. See this process in action by watching this tutorial!
How Do You Use a Graph to Translate a Figure Diagonally?

Performing multiple translations on the graph of a figure is easier than you might think! In this tutorial, see how to use the graph of the original figure to perform each translation in order to get the graph of the new figure. Check it out!
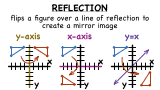
What is a Reflection?

When you look in the mirror, you see your reflection. In math, you can create mirror images of figures by reflecting them over a given line. This tutorial introduces you to reflections and shows you some examples of reflections. Take a look!
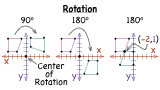
What is a Rotation?

Ever turned a door handle? You were performing a rotation! In math, rotations are just the same! Check out this tutorial to learn about rotations.
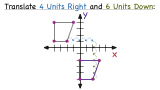
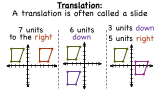
What is a Translation?

Ever slide something across a table? If so, then you have performed a translation! In this tutorial, learn the definition of translation and see some really neat examples. Take a look!
What is Rotational Symmetry?

Ever notice that some shapes look the same after you rotate them? These shapes have a property called rotational symmetry! Check out this tutorial to learn more.
What is Line Symmetry? Sate

When a shape looks the same after a reflection, that shape has a property called line symmetry. In this tutorial you'll see that some shapes have reflectional symmetry, and some don't. Check it out!