Texas Geometry

More Specific Topics in Texas Geometry

Popular Tutorials in Texas Geometry

What are Similar Figures?

Looking at two figures that are the same shape and have the same angle measurements? You have similar figures! Learn all about it in this tutorial!
How Do You Solve a Problem Using Indirect Measurement with Shadows?

Word problems allow you to see the real world uses of math! This tutorial shows you how to take a word problem and use indirect measurement to turn it into a proportion. Then see how to use the mean extremes property of proportions to cross multiply and solve for the answer. Take a look!
How Do You Identify Transformations in the Equation of a Rational Function?

If you can figure out how the equation of a rational function was transformed, then you can make a good sketch of that function without finding lots of individual points. Take a look at the video to learn more!
What is the Parent Function for a Rational Function?

Like linear, quadratic, and cubic functions, rational functions also have a parent. It's also the parent function for the reciprocal function family. Check out this tutorial to learn more about its characteristics!
How Do You Know if Two Lines are Parallel?

Parallel lines are lines that will go on and on forever without ever intersecting. This is because they have the same slope! If you have two linear equations that have the same slope but different y-intercepts, then those lines are parallel to one another!
How Do You Know if Two Lines Are Perpendicular?

Perpendicular lines intersect at right angles to one another. To figure out if two equations are perpendicular, take a look at their slopes. The slopes of perpendicular lines are opposite reciprocals of each other. Their product is -1! Watch this tutorial and see how to determine if two equations are perpendicular.
What's the Midpoint Formula?

Want to find the point midway between two locations? Then you're looking for the midpoint! The midpoint of a line segment is the point located midway between the endpoints of the line segment. This tutorial tells you about the midpoint of a line segment. Take a look!
What's Slope-Intercept Form of a Linear Equation?

When you're learning about linear equations, you're bound to run into the point-slope form of a line. This form is quite useful in creating an equation of a line if you're given the slope and a point on the line. Watch this tutorial, and learn about the point-slope form of a line!
How Do You Find the Distance Between Two Points?

Trying to find the distance between two points? Use the distance formula! Want to see how it's done? Check out this tutorial!
What are the Legs and Hypotenuse of a Right Triangle?

Looking for some terminology used with right triangles? Then this tutorial was made for you! In this tutorial, you'll be introduced to the names for the different parts of a right triangle. Check it out!
What is the Converse of the Pythagorean Theorem?

The converse of the Pythagorean Theorem is like the the Pythagorean Theorem in reverse. You can use it both forward and backward! Not all theorems work this way, but the Pythagorean Theorem does! This tutorial will show you how to use both the Pythagorean Theorem and its converse.
What Is the Distance Formula?

If you need to find the distance between to points on the coordinate, you'll probably use the distance formula to get your answer. This tutorial introduces you to the distance formula and even shows you how to find it!
What is the Pythagorean Theorem?

The Pythagorean theorem is a very popular theorem that shows a special relationship between the sides of a right triangle. In this tutorial, you'll get introduced to the Pythagorean theorem and see how it's used to solve for a missing length on a right triangle!
How Do You Find the Probability of a Simple Event?

Working with probabilities? Check out this tutorial! You'll see how to calculate the probability of picking a certain marble out of a bag.
How Do You Find the Probability of Independent Events?

Calculating probabilities? Take a look at this tutorial and see how to figure out the probability of independently drawing certain cards from a deck!
How Do You Find the Probability of Dependent Events?

Sometimes probabilities depend on the outcomes of other events. Check out this tutorial to see probabilities of dependent events in action!
How Do You Solve a Word Problem Using the Permutation Formula?

Permutations occur in real life all the time! Want to know how many ways you can choose a certain number of items when the order matters? Then you need to calculate the number of permuations. Check out this tutorial to see how.
What is the Fundamental Counting Principle?

The Fundamental Counting Principle is a way to figure out the total number of ways different events can occur. In this tutorial, you'll be introduced to this principle and see how to use it in an example. Take a look!
What is Experimental Probability?

Do real life situations always work out the way your mathematical models tell you they should? No! This tutorial describes how experimental probability differs from theoretical probability.
What is the Distributive Property?

The distributive property is a very deep math principle that helps make math work. It's the rule that lets you expand parentheses, and so it's really critical to understand if you want to get good at simplifying expressions. So check out the tutorial and let us know what you think!
How Do You Solve a Word Problem Using a Proportion?

This tutorial provides a great real world application of math. You'll see how to use the scale from a blueprint of a house to help find the actual height of the house. This tutorial shows you how to use a proportion to solve!
What is a Theorem?

Theorems are a way for mathematicians to make a general mathematical statement. These statements can be used to help you solve all sorts of problems! See an introductions to theorems with this tutorial.
How Do You Graph the Natural Base Exponential Function?

Want to graph a natural base exponential function? Make a table of points! Then plot the points, connect them, and you have your graph! Follow along with this tutorial to see the entire process step-by-step.
What is the Natural Base Exponential Function?

The natural base exponential function is actually a function that's shorter than its name! This tutorial introduces you to this special function and shows you what it looks like.
How Do You Graph a Rational Function by Finding its Asymptotes and Zeros?

In a rational function, the denominator of the rational expression holds the key to the location of the vertical asymptotes. The relationship between degrees of the numerator and denominator determine the nature of the horizontal asymptotes. Check out the tutorial to learn more!
How Do You Use the Equation for a Rational Function to Find Its Horizontal Asymptotes?

Rational functions behave predictably as they head off to infinity. Follow this tutorial to learn more about their asymptotic behavior!
How Do You Write an Equation For a Circle If You Know its Center and Radius?

Writing an equation for a circle is easy if you know how! Check out this tutorial to see how you can write the equation of a circle if you know its center and radius.
What is a Circle?

What exactly is a circle? Learn the answer in this tutorial. You can also see the equation for a circle that's on the coordinate plane!
How Do You Find Conditional Probability?

Conditional probability is used to find a probability in all sorts of everyday situations! This tutorial shows you one example of how to find the conditional probability in a real world problem.
What is Conditional Probability?

If you're learning about probability, conditional probability is bound to come up. This tutorial explains conditional probability and shows you how to find it!
How Do You Convert from Degrees to Radians?

There is a simple formula to convert between degrees and radians. But to remember the formula, it helps to understand the relationship between degree and radians. Check out this tutorial to learn more!
What is the Sine Ratio?

The sine ratio is a handy ratio when you're dealing with right triangles! In this tutorial, you'll learn what the sine ratio is and how to use it to find angle measurements in a right triangle.
What is the Tangent Ratio?

There are several different ratios you can make from the sides of a right triangle. One of them is the tangent ratio. Watch this tutorial to add the tangent ratio to your right triangle tool box!
What is a Radian?

You already know that you can use degrees to measure angles. Radians are just another way of doing the same thing! But there is a special relationship that makes radians a more natural way to measure angles than degrees. Check out this tutorial to learn more!
What is the Formula for the Area of a Triangle Using Sines?

You can use sine to help you find the area of a triangle! All you need is two sides and an angle measurement! This tutorial helps you find this formula.
What is the Segment Addition Postulate?

You've known how to add numbers for a long time. The Segment Addition Postulate extends this operation to lengths of line segments. However, there is a catch. Watch the tutorial to find out what it is!
How Do You Write the Converse, Inverse, and Contrapositive of a Conditional Statement and Determine Their Truth Values?

A conditional statement is an if-then statement. For every conditional statement you can write three related statements, the converse, the inverse, and the contrapositive. The video shows how these are related.
How Do You Write a Biconditional Statement?

If you can write a true statement using "if and only if" , then you've got a biconditional. Learn more about biconditionals by watching the video.
How Do You Identify the Hypothesis and Conclusion of a Conditional Statement in If-Then Format?

People use hypotheses and conclusions all of the time, often without realizing it. Every conditional if-then statement is composed of a hypothesis and a conclusion. Check out the tutorial to learn more!
How Do You Use the Law of Detachment to Draw a Valid Conclusion?

See the Law of Detachment in action! This tutorial shows you an example that uses the Law of Detachment to make a conclusion.
How Do You Use Vertical Angles to Find Angle Measures Using Algebra?

When two lines or segments intersect, two pairs of vertical angles are formed. By the Vertical Angle Theorem, vertical angles are congruent. If you have algebraic expressions for the measures of the vertical angles, you can use the Vertical Angle Theorem to solve for their measures. Check out the tutorial to learn more!
What is Inductive Reasoning?

You probably observe data and patterns to make predictions or conjectures on a regular basis. If so, you are using inductive reasoning. Check out the video to learn more!
What is the Law of Syllogism?

If you have related conditional statements, the Law of Syllogism can help you link those conditional statements into one conditional statement. In this tutorial, you'll see how to combine related conditional statements using the Law of Syllogism.
What is a Biconditional Statement?

When a conditional statement and its converse are both true, you can write them as one statement called a biconditional statement. Learn more about this special kind of statement by following along with this tutorial.
What is a Counterexample?

It can be really tough to prove a conjecture to always be true, but it only takes one good counterexample to prove it false! Watch the tutorial to find out about counterexamples.
How Do You Use Parallel and Perpendicular Theorems to Prove a Relationship Between Two Lines?

Parallel and perpendicular lines can be found in all sorts of places! In this tutorial, see how to use your knowledge of parallel and perpendicular lines to solve a word problem.
How Do You Construct a Line Parallel to Another Line Through a Given Point?

A compass is a very handy tool! In this tutorial, you'll see how to use a compass and straightedge to construct parallel lines!
How Do You Construct a Line Perpendicular to Another Line Through a Given Point On the Line?

Trying to draw a line perpendicular to another line through a given point, but don't have a protractor? No problem, as long as you have a compass and a straightedge! To see the whole process, watch the video.
What is the Corresponding Angles Postulate?

When a transversal intersects parallel lines, the corresponding angles created have a special relationship. The corresponding angles postulate looks at that relationship! Follow along with this tutorial to learn about this postulate.
What is the Converse of the Corresponding Angles Postulate?

The corresponding angles postulate states that when a transversal intersects parallel lines, the corresponding angles are congruent. What if you go the other way and start with corresponding angles that are congruent? Is the converse of this postulate true? This tutorial explores exactly that!
How Do You Determine if Triangles on the Coordinate Plane are Congruent?

There are many ways to show that two triangles are congruent. This tutorial shows you how to use a triangle congruence postulate to show that two triangles on the coordinate plane are congruent to each other!
How Do You Use a Congruence Postulate to Prove Triangles are Congruent?

When proving two triangles are congruent, you use information and postulates you already know to create a logical trail from what you know to what you want to show. This tutorial shows an example of using a congruence postulate to show two triangles are congruent!
How Do You Show that Corresponding Parts of Congruent Triangles are Congruent?

If you're given information about two triangles and asked to prove parts of the triangles are congruent, see if you can show the two triangles are congruent. If they are, then you know that the corresponding parts are congruent! Follow along with this tutorial to see an example.
How Do You Prove that Two Overlapping Triangles are Congruent?

Proofs are an important part of geometry. This tutorial shows you how to use given information to prove that two overlapping triangles are congruent!
How Do You Identify Common Parts in Overlapping Triangles?

It might seem like a challenge to make sense of figures with overlapping triangles, but it's not so difficult! This video gives some commonsense advice for identifying common angles and common sides in these figures.
What is the Side-Angle-Side Postulate for Triangle Congruence?

The Side-Angle-Side postulate is just one of many postulates you can use to show two triangles are congruent. This tutorial introduces you to the SAS postulate and shows you how to use it!
What is the Angle-Side-Angle Postulate for Triangle Congruence?

What is the Angle-Side-Angle postulate? This postulate is just one of many postulates you can use to prove two triangles are congruent! This tutorial explains the ASA postulate.
What is CPCTC?

The term CPCTC can come up a lot when you're dealing with congruent triangles, but what does it mean? This tutorial gives a great explanation and shows you how to use it in an example!
What is the Hypotenuse-Leg Congruence Theorem?

There's a special theorem that helps you quickly figure out if two right triangles are congruent. This tutorial introduces you to that theorem and shows you how to use it!
How Can You Tell if a Point is on the Perpendicular Bisector of a Line Segment?

If you want to determine if a point is on the perpendicular bisector of a line segment, the Perpendicular Bisector Theorem and its converse might come in handy. This tutorial gives a great example of how to tell if a given point is a perpendicular bisector of a segment!
How Do You Use the Centroid to Find Segment Lengths in a Triangle?

When you're given the centroid of a triangle and a few measurements of that triangle, you can use that information to find missing measurements in the triangle! This tutorial shows you how it's done.
How Do You Determine Whether a Triangle Can Be Formed Given Three Side Lengths?

If you're given 3 side measurements, there's a quick way to determine if those three sides can form a triangle. Follow along with this tutorial and learn what relationship these sides need in order to form a triangle.
How Do You Use the Hinge Theorem to Compare Side Lengths in Two Triangles?

The Hinge Theorem helps you compare side measurements of two triangles when you have two sets of congruent sides. Follow along with this tutorial to see this theorem used to find the relationship between the sides of two triangles.
How Do You Construct a Perpendicular Bisector?

This tutorial shows you how to construct a perpendicular bisector using only a compass and a straightedge!
How Do You Write an Indirect Proof?

This tutorial looks at using an indirect proof to show that an equilateral triangle cannot have a right angle.
How Do You Use the Perpendicular Bisector Theorem to Find Measures of Lengths in Triangles?

When solving for length or angle measures in triangles, theorems you have learned previously can come in handy! Watch this tutorial to find out how to use the Perpendicular Bisector Theorem to find out the side lengths of a triangle.
How Do You Put the Sides of a Triangle in Order According to Size if You Know Two Angles of the Triangle?

Trying to figure out which side of a trianlge is the shortest? How about the longest? All you need to get your answer are the angle measurements of the triangle! How does it work? Watch this tutorial to find out!
What is the Midsegment of a Triangle?

A triangle has three sides and each of them has a midpoint. Choose any two midpoints, connect them, and now you have a midsegment! Watch the tutorial to learn more.
What is the Circumcenter of a Triangle?

This tutorial explains the ins and outs of the circumcenter of a triangle. You'll see how to build up from the Perpendicular Bisector Theorem to find the circumcenter of a triangle.
What is the Incenter of a Triangle?

The incenter of a triangle deals with the angle bisectors of a triangle. This tutorial shows you how to find the incenter of a triangle by first finding the angle bisectors.
What is an Indirect Proof?

Indirect proofs can be a tricky, but they are an essential part of your proof writing tool kit. Mastering this technique is an important step in your mathematical journey! Check out this tutorial to learn more.
What is the Hinge Theorem?

What's the Hinge Theorem all about? Watch this tutorial to find out!
What is the Triangle Midsegment Theorem?

The triangle midsegment theorem looks at the relationship between a midsegment of a triangle and the triangle's third side. Follow along with this tutorial to learn about the triangle midsegment theorem.
What is a Median of a Triangle?

A median of a triangle is a special line segment that connects two pieces of a triangle. This tutorial introduces you to the median of a triangle and shows you how many medians each triangle has!
How Do You Find Values for Variables in the Angles of a Quadrilateral To Make it a Parallelogram?

When you're given a quadrilateral with some of the interior angles defined with variables, you can find what values those variables need to have to make that quadrilateral a parallelogram. Follow along with this tutorial to learn what steps to take to get the answer!
How Do You Use the Diagonals of a Rectangle to Find the Value of a Variable?

When you make diagonals inside a rectangle, those diagonals are congruent. With this information, you can find the value of a variable that's part of a measurement of a diagonal. This tutorial shows you the steps.
How Do You Use Variables to Name Coordinates for a Figure Placed on the Coordinate Plane?

This tutorial shows you how to find the vertices of a rhombus that's graphed on the coordinate plane!
How Do You Write a Coordinate Proof?

In this tutorial, you'll see how to write a coordinate proof to prove that two triangles are congruent. Check it out!
How Do You Find the Values of Variables in a Parallelogram Diagram?

There are a lot of theorems to help you find missing measurements in a parallelogram diagram! Watch this tutorial find out more!
How Do You Find the Value for a Variable in the Angles of a Quadrilateral To Make it a Rhombus?

A parallelogram needs to have certain qualities in order to be a rhombus. In this tutorial, you'll use your knowledge of these shapes in order to find the value for a variable that will make a given parallelogram a rhombus.
How Do You Find a Value for a Variable in a Trapezoid?

There are a lot of theorems to help you find missing measurements in a trapezoid diagram! Watch this tutorial find out more!
How Do You Position a Figure on the Coordinate Plane for a Coordinate Proof?

When you are placing a figure on a coordinate plane for a coordinate proof, you want to choose your points to make calculations easy, while still allowing for a completely general description of the figure in question. Check out this tutorial to find out how!
How Do You Use the Triangle Proportionality Theorem to Find Missing Lengths in a Diagram?

This tutorial shows you how the Triangle Proportionality Theorem can be used to find a missing length in a diagram. Take a look!
How Do You Use the Angle Bisector Theorem to Find Missing Side Lengths in a Diagram?

There are lots of special lines in triangles that can help you solve for side lengths and angle measures. Watch this tutorial to find out how to use the Angle Bisector Theorem to find missing side lengths in triangles!
How Do You Determine if Two Triangles are Similar Using the SAS Similarity Postulate?

What does SAS mean? The position of the letters gives you a clue as to how to use the SAS Similarity Postulate! Check out this tutorial to learn more.
How Do You Find a Geometric Mean?

To find the geometric mean of two numbers, just find the product of those numbers and take the square root! Follow along with this tutorial to learn the process step-by-step.
What is a Geometric Mean?

The geometric mean can help you find a missing term in a geometric sequence. Before you find the geometric mean, you should understand what it is. This tutorial defines geometric mean.
How Do You Graph a Glide Reflection?

When you graph a composition of two transformations, you have to be very careful to perform all the steps in the right order! Watch this tutorial to see how to graph a glide reflection.
How Do You Identify a Congruence Transformation?

Want to figure out whether two figures are congruent? There's a mathematically precise way to do this! Watch this tutorial on congruence transformations to learn more.
How Do You Identify a Similarity Transformation?

How do you know if one figure is similar to another? If you can find a similarity transformation that maps one figure to the other, then the figures are similar! Learn more about spotting similarity transformations with this tutorial.
How Do You Graph a Translation Then a Dilation?

When you graph a composition of two transformations, you have to be very careful to perform all the steps in the right order! Watch this tutorial to see how to graph a translation of a figure, followed by a dilation.
What is a Congruence Transformation, or Isometry?

Not all transformations are created equal! Congruence transformations, or isometries, have a special property that distinguishes them from other transformations. This tutorial will show you what makes them special!
What Makes Two Figures Congruent?

When are two figures congruent? When you can move one on top of the other without changing its size or shape! Check out this tutorial to learn more about using isometries to map congruent figures onto each other.
How Do You Determine Whether Two Chords are Equidistant From the Center of a Circle?

When you want to know if two chords are the same distance away from the center of the circle, there's a quick way to get the answer. In this tutorial, you'll learn how to find that answer and figure out which chords are equidistant from the center.
How Do You Find The Measure of an Inscribed Angle When You Know the Measure of the Intercepted Arc?

When you're given the measurement of the intercepted arc, you can find the measure of the inscribed angle with a few short steps! Follow along with this tutorial to learn how to find an inscribed angle when you know the intercepted arc!
How Do You Use Intersecting Chords to Find Arc Measures in a Circle?

This tutorial shows you how to use your knowledge of intersecting arcs in a circle to find a missing arc measurement. Take a look!
How Do You Find the Measure of an Angle Created by Intersecting Chords in a Circle?

This tutorial shows you how to use your knowledge of intersecting chords in a circle to find a missing angle measurement.
How Do You Determine Whether a Line is Tangent to a Circle?

In this tutorial, you'll see how the Converse of the Pythagorean Theorem is used to figure out if a line is tangent to a circle.
How Do You Find the Length of a Chord in a Circle if You're Given another Chord Equidistant from the Center?

Chords, diameters, arcs, and central angles all have special relationships in a circle. This tutorial will help you make some sense of it all!
How Do You Find Missing Measures of Angles in Quadrilaterals Inscribed in Circles?

When a quadrilateral is inscribed in a circle, you can find the angle measurements of the quadrilateral in just a few quick steps! Follow along with this tutorial to learn what to do!
What is a Tangent Line to a Circle?

What does it mean when a line is tangent to a circle? In this tutorial, you'll learn what a line needs to do to be a tangent line to a circle.
How Do You Find the Area of a Regular Polygon When You Know the Length of the Apothem?

If you need to find the area of a regular polygon all you need is the apothem! This tutorial shows you how to find the area of a regular pentagon when you only know the apothem.
How Do You Use Similar Figures to Find the Area of a Polygon?

When you're working with similar figures, knowing the scale factor can help you find all sorts of pieces including side measurements and area. This tutorial shows you how to use the scale factor to help find the area of one of the figures.
How Do You Find Geometric Probability Using Areas?

This tutorial gives you practice finding geometric probability. Given a circle inscribed in a square, you'll see how to find the probability that a point chosen at random will land in the circle!
How Do You Find the Scale Factor Between Two Polygons if You Know Their Areas?

The scale factor between two similar polygons is not the same as the ratio of their areas. It's a bit more complicated than that! This tutorial will show you how to find the correct scale factor.
How Do You Find the Area of a Regular Polygon When You Know the Length of One Side?

It might surprise you to learn that all you need to know to find the area of a regular polygon is one side length and the number of sides. It's true! Watch this tutorial to find out how.
What is the Area Probability Ratio?

If one region of a plane figure is entirely within another, the ratio of the smaller area to the larger is a number between 0 and 1. Sounds like a probability! This tutorial will help you learn about the area probability ratio.
What is the Substitution Property of Equality?

If you ever plug a value in for a variable into an expression or equation, you're using the Substitution Property of Equality. This property allows you to substitute quantities for each other into an expression as long as those quantities are equal. Watch this tutorial to learn about this useful property!
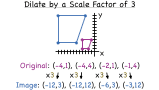
How Do You Make a Figure Larger Using a Dilation?

Dilation allows you to shrink or enlarge the size of a figure without changing its shape. In this tutorial, follow along as you see how dilate a figure by a given scale factor. Check it out!
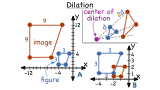
What is a Dilation?

When someone's eyes dilate, their pupils get bigger or smaller, but they always stay the same shape. Dilation in math is very similar. When you dilate a figure, you change the size of the figure without changing its shape. This tutorial introduces you to dilation. Take a look!
How Do You Write the Equation of a Line in Slope-Intercept Form If You Have a Graph?

Working with the graph of a line? Trying to find the equation for that graph? Just pick two points on the line and use them to find the equation. This tutorial shows you how to take two points on the graph of a line and use them to find the slope-intercept form of the line!
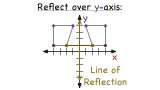
How Do You Use a Graph to Reflect a Figure Over the Y-Axis?

Reflecting a figure over the y-axis can be a little tricky, unless you have a plan. In this tutorial, see how to use the graph of a figure to perform the reflection. Check it out!
How Do You Find Missing Angles in an Isosceles Triangle?

Trying to find a missing interior angle measurement in a triangle? See if you're working with a special type of triangle such as an equilateral or isosceles triangle. If you are, that knowledge can help you. In this tutorial, see how identifying your triangle first can be very helpful in solving for that missing measurement. Take a look!
How Do You Find Missing Angles in a Triangle With Variables?

Looking for the measurements of the interior angles of a given triangle? The Triangle Sum theorem might help. This theorem states that the interior angles of a triangle ALWAYS add up to 180 degrees! This tutorial shows you how to use that information to find those interior angle measurements.
How Do You Find the Angle Measures of a Regular Polygon?

You can use what you already know to find out the angle measures of regular polygons! Watch this tutorial to find out how.
How Do You Identify Corresponding Parts in Congruent Triangles?

When you have two congruent figures, that means that corresponding sides and corresponding angles are congruent. Get some practice identifying corresponding sides and angles by following along with this tutorial!
How Do You Write a Congruence Statement for Congruent Triangles?

Once you've identified corresponding parts in congruent triangles you have the information you need to write a congruence statement for the triangles. Follow the tutorial to learn how to choose your vertices wisely!
How Do You Find Missing Angles in an Isosceles Triangle Using Right Triangles?

Trying to find a missing interior angle measurement in a triangle? See if you're working with a special type of triangle such as an equilateral or isosceles triangle. If you are, that knowledge can help you. In this tutorial, see how identifying your triangle first can be very helpful in solving for that missing measurement. Take a look!
How Do You Find Missing Angles in a Transversal Diagram?

Got a diagram of a transversal intersecting parallel lines? Trying to figure out all the angle measurements? Take a look at this tutorial, and you'll see how find all the missing angle measurements by identifying vertical, corresponding, adjacent, and alternate exterior angles!
How Do You Find a Value for x that Makes Two Lines Parallel?

Got a transversal intersecting two lines? Trying to figure out if those lines are parallel? You could test to see if corresponding angles are congruent. This tutorial shows you how!
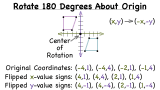
How Do You Rotate a Figure 180 Degrees Around the Origin?

Rotating a figure about the origin can be a little tricky, but this tutorial can help! This tutorial shows you how to rotate coordinates from the original figure about the origin. Then, simply connect the points to create the new figure. See this process in action by watching this tutorial!
How Do You Use a Graph to Translate a Figure Diagonally?

Performing multiple translations on the graph of a figure is easier than you might think! In this tutorial, see how to use the graph of the original figure to perform each translation in order to get the graph of the new figure. Check it out!
What is a Rectangle?

A rectangle is one of the many fundamental shapes you'll see in math. Rectangles have special properties that can be very useful in helping you solve a problem. This tutorial introduces you to rectangles and explains their interesting qualities!
What is a Parallelogram?

A parallelogram is a special type of quadrilateral with some special properties. In this tutorial, take a look at parallelograms and learn what kinds of quadrilaterals can also be called parallelograms!
What is a Trapezoid?

A trapezoid is a special type of quadrilateral with some special properties. This tutorial introduces you to trapezoids and gives you a look at the special properties needed for a quadrilateral to be called a trapezoid. Check it out!
What is a Point?

A point is a fundamental building block of math. Without points, you couldn't make lines, planes, angles, or polygons. That also means that graphing would be impossible. Needless to say, learning about points is very important! That makes this tutorial a must see!
What is a Plane?

You can't learn everything about math without seeing planes. Did you know that there are rules for naming a plane? This tutorial introduces you to planes and shows you how to name them. Take a look!
What is an Angle?

Angles are a fundamental building block for creating all sorts of shapes! In this tutorial, learn about how an angle is formed, how to name an angle, and how an angle is measured. Take a look!
What are Acute, Obtuse, Right, and Straight Angles?

Did you know that there are different kinds of angles? Knowing how to identify these angles is an important part of solving many problems involving angles. Check out this tutorial and learn about the different kinds of angles!
What are Supplementary Angles?

Knowing about supplementary angles can be very useful in solving for missing angle measurements. This tutorial introduces you to supplementary angles and shows you how to use them to solve for a missing angle measurement. Take a look!
What are Vertical Angles?

Vertical angles have a very special quality. They are always congruent to one another! Check out this tutorial to learn about and see how to identify vertical angles!
What Does Congruent Mean?

If two figures have the same size and shape, then they are congruent. The term congruent is often used to describe figures like this. In this tutorial, take a look at the term congruent!
What are Parallel Lines?

Lines that are parallel have a very special quality. Without this quality, these lines are not parallel. In this tutorial, take a look at parallel lines and see how they are different from any other kind of lines!
What are Perpendicular Lines?

Perpendicular lines have a special property. The angles formed by perpendicular lines will always be the same. Check out this tutorial to learn about perpendicular lines and see a cool trick involving these special lines!
What are Skew Lines?

Ever heard of skew lines? They're pretty cool! Take a look at this tutorial and you'll be introduced to skew lines.
What are Equilateral, Isosceles, and Scalene Triangles?

Did you know that there are different kinds of triangles? Knowing how to identify these triangles is an important part of solving many problems involving these triangles. Check out this tutorial and learn about some of the different kinds of triangles!
What is a Reflection?

When you look in the mirror, you see your reflection. In math, you can create mirror images of figures by reflecting them over a given line. This tutorial introduces you to reflections and shows you some examples of reflections. Take a look!
What is a Rotation?

Ever turned a door handle? You were performing a rotation! In math, rotations are just the same! Check out this tutorial to learn about rotations.
What is a Translation?

Ever slide something across a table? If so, then you have performed a translation! In this tutorial, learn the definition of translation and see some really neat examples. Take a look!
What is Rotational Symmetry?

Ever notice that some shapes look the same after you rotate them? These shapes have a property called rotational symmetry! Check out this tutorial to learn more.
What is Line Symmetry? Sate

When a shape looks the same after a reflection, that shape has a property called line symmetry. In this tutorial you'll see that some shapes have reflectional symmetry, and some don't. Check it out!
How Do You Find the Sum of the Interior Angles of a Polygon?

Polygons have all kinds of neat properties! For example, if you know the number of sides of a polygon, you can figure out the sum of the interior angles. That knowledge can be very useful when you're solving for a missing interior angle measurement. Check out this tutorial to learn how to find the sum of the interior angles of a polygon!
What is the Triangle Sum Theorem?

When you're dealing with triangles, the Triangle Sum theorem can be very useful in finding interior angle measurements. In this tutorial, learn how to find this helpful theorem!
How Do You Solve a Problem Using an Angle of Elevation?

This tutorial provides a great real world application of math. You'll see how to use the tangent ratio to find the height of a hill. Take a look!
How Do You Solve a Problem Using an Angle of Depression?

Trigonometric ratios help you solve all kinds of real-world math problems. Check out this tutorial to see how to solve problems that deal with angles of depression!
What is a 45Â°-45Â°-90Â° Triangle?

A 45-45-90 triangle is a special right triangle with some very special characteristics. If you have a 45-45-90 triangle, you can find a missing side length without using the Pythagorean theorem! Check out this tutorial to learn about 45-45-90 triangles!
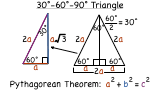
What is a 30-60-90 Degree Triangle?

A 30-60-90 triangle is a special right triangle with some very special characteristics. If you have a 30-60-90 degree triangle, you can find a missing side length without using the Pythagorean theorem! Check out this tutorial to learn about 30-60-90 triangles!
How Do You Find the Area of a Trapezoid?

Want to find the area of a trapezoid? If you have the length of each base and the height, you can use them to find the area. In this tutorial, you'll see how to identify those values and plug them into the formula for the area of a trapezoid. Then see how to simplify to get your answer!
How Do You Find the Area of a Sector of a Circle?

Trying to find the area of a sector of a circle? Then check out this tutorial! You'll see how to use given information and the formula for the area of a sector to find the answer. Take a look!
How Do You Find the Volume of a Cylinder?

The volume of a cylinder is the amount of space that will fit inside it. You can use the formula for the volume of a cylinder to find that amount! In this tutorial, see how to use that formula and the radius and height of the cylinder to find the volume. Check it out!
How Do You Find the Volume of a Cone?

To find the volume of a cone, you need to plug in the measurement for the height of the cone and the radius of the base into the formula for the volume of a cone. Then simplify to get your answer. This tutorial shows you the entire process step-by-step!
How Do You Find the Volume of a Sphere?

Want to find the volume of a sphere? If you know the radius of the sphere, you can simply plug that value into the formula for the volume of a sphere and simplify! This tutorial shows you how!
How Do You Find the Lateral and Surface Areas of a Rectangular Prism?

The lateral area of a three-dimensional solid is the area of all the lateral faces. In this tutorial, you'll see how to use the dimensions of a rectangular prism to find the lateral area. Take a look!
How Do You Find the Lateral and Surface Areas of a Cylinder?

Want to know how the find the lateral and surface areas of a cylinder? Then this tutorial was made for you! You'll see how to apply each formula to the given information to find the lateral area and surface area. Check it out!
How Do You Find the Lateral and Surface Areas of a Regular Pyramid?

Want to know how the find the lateral and surface areas of a regular pyramid? Then this tutorial was made for you! You'll see how to apply each formula to the given information to find the lateral area and surface area. Check it out!
How Do You Find the Lateral and Surface Areas of a Cone?

Want to know how the find the lateral and surface areas of a cone? Then check out this tutorial! You'll see how to apply each formula to the given information to find the lateral area and surface area. Take a look!
How Do You Find the Surface Area of a Sphere?

Trying to find the surface area of a sphere? Already know the radius? Then plug that value into the formula for the surface area of a sphere and solve to get the answer! This tutorial shows you how!
How Do You Find Volumes of Similar Solids?

There's a way to find out the ratio of the volumes of similar solids â€” but it's not as simple as comparing the sides. Watch this tutorial to find out how!
What is a Circle?

Circles are a fundamental part of math! In this tutorial, you'll be introduced to circles and see the different parts of a circle such as the diameter, radius, and chord. Check out this tutorial to learn about circles!
What is a Solid?

Understanding solids is a building block for finding their lateral area, surface area, and volume. In this tutorial, you'll see examples of solids and learn their different parts. Take a look!
What is a Sphere?

Every played with a bouncy ball, a volleyball, a basketball, or a baseball? Those are all spheres! Check out this tutorial to see what defines a sphere and learn its different parts. Take a look!
What is the Relationship Between the Surface Areas of Similar Solids?

If you have similar solids, there's a ratio that relates their surface areas. This tutorial uses similar prisms to help you find the ratio rule of the surface areas of any similar solids!
What is the Formula for the Area of a Triangle?

Did you know that the formula for the area of a triangle can be found by using the formula for the area of a parallelogram? In this tutorial, you'll see how it's done! Take a look!
What is the Formula for the Area of a Parallelogram?

Parallelograms and rectangles are pretty similar. In fact, you can turn a parallelogram into a rectangle to find the formula for the area of a parallelogram! Check out this tutorial to see how it's done!
What is the Formula for the Area of a Trapezoid?

Trying to figure out the formula for the area of a trapezoid? You could start by creating a parallelogram out of two trapezoids. Then, use the formula for the area of a parallelogram to figure out the formula for the area of one trapezoid. This tutorial shows you how!
What is Circumference?

The circumference of a circle is the distance around that circle. But what is the formula to find the circumference? In this tutorial, you'll learn the formulas for the circumference of a circle. Take a look!
What is the Formula for the Area of a Circle?

Did you know that you can figure out the formula for the area of a circle by first turning the circle into a parallelogram? It seems a little weird, but it really works! Watch this tutorial to see how it's done!
What is the Formula for the Volume of a Prism?

Trying to find the volume of a prism? Did you know that there's a formula to find that volume? In this tutorial, you'll learn about the formula for the volume of a prism. Check it out!
What is the Formula for the Volume of a Pyramid?

Looking for the formula for the volume of a pyramid? Then check out this tutorial! You'll learn about the formula for the volume of a pyramid and see how to use the formula in an example. Take a look!