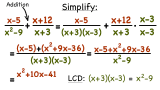Texas Algebra 2
More Specific Topics in Texas Algebra 2
Popular Tutorials in Texas Algebra 2
-
How Do You Use a Compound Sentence to Solve an Absolute Value Equation?
The trick to solving an absolute value equation is to rewrite it as a compound sentence. Watch this tutorial to find out more!
-
How Do You Graph an Absolute Value Function?
Graphing an absolute value equation can be complicated, unless you know how to dissect the equation to find and use the slope and translations. Follow along as this tutorial shows you how to identify the necessary parts of the equation and use them to graph the absolute value equation.
-
How Do You Solve a Greater Than Absolute Value Inequality and Graph It On a Number Line?
An absolute value inequality containing a "greater than" or "greater than or equal to" symbol requires careful reasoning and a special set of steps to find and graph its solutions. Follow along with this tutorial to find out more!
-
What is the Parent Function Graph for Absolute Value?
Lots of function families have parent functions, and the family of absolute value functions is no exception. The parent graph for absolute value has a unique shape that you won't find anywhere else. Watch this tutorial to learn more!
-
What Does the Constant 'k' do in y = |x|+k?
When you're learning about translating absolute value equations, learning about vertical translations is a MUST! Check out this tutorial and see what it takes to translate an absolute value equation vertically.
-
How Do You Solve an Absolute Value Equation with One Solution?
Some absolute value equations have only one solution. Watch this tutorial to learn how to solve them!
-
What is an Absolute Value Function?
An absolute value function is just a function that contains absolute values. This tutorial gives a great introduction to this very useful function!
-
How Do You Write a Rule for a Geometric Sequence?
Trying to find the value of a certain term in a geometric sequence? Use the formula for finding the nth term in a geometric sequence to write a rule. Then use that rule to find the value of each term you want! This tutorial takes you through it step-by-step.
-
What Does the Constant 'h' Do in the Exponential Function f(x)=bx-h?
The constants in an exponential function affect the function's graph in different ways. Watch the tutorial to see how one such constant can translate the graph of an exponential function left or right.
-
What Does the Value of 'a' Do in the Exponential Function f(x)= a (bx)?
Multiplying an exponential function by a constant changes the function's graph. Watch the tutorial to find out how!
-
What's an Exponential Function?
Looking at an equation with a variable in the exponent? You have an exponential function! Learn about exponential functions in this tutorial.
-
What is Exponential Growth?
Exponential functions often involve the rate of increase or decrease of something. When it's a rate of increase, you have an exponential growth function! Check out these kinds of exponential functions in this tutorial!
-
How Do You Factor a Trinomial?
Factoring trinomials can by tricky, but this tutorial can help! Follow along as a trinomial is factored right before your eyes! Then, check your answer by using the FOIL method to multiply the binomials back together and see if you get the original trinomial.
-
How Do You Solve a Rational Equation by Adding Fractions?
Want some extra practice solving rational equations? This tutorial gives you just that! You'll see how to solve a rational equation containing rational expressions with common denominators. Then, you'll see how to solve an equation containing rational expressions with unlike denominators. Take a look!
-
How Do You Solve a Rational Equation by LCD Multiplication?
Want some extra practice solving rational equations? This tutorial gives you just that! You'll see how to solve a rational equation containing rational expressions with common denominators. Then, you'll see how to solve an equation containing rational expressions with unlike denominators. Take a look!
-
How Do You Divide Two Polynomials by Factoring and Canceling?
Simplifying a rational expression? You could factor the numerator and denominator and then cancel like factors. Learn what to do in this tutorial!
-
How Do You Identify Transformations in the Equation of a Rational Function?
If you can figure out how the equation of a rational function was transformed, then you can make a good sketch of that function without finding lots of individual points. Take a look at the video to learn more!
-
What is the Parent Function for a Rational Function?
Like linear, quadratic, and cubic functions, rational functions also have a parent. It's also the parent function for the reciprocal function family. Check out this tutorial to learn more about its characteristics!
-
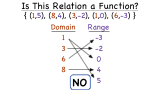
How Can You Tell if a Relation is Not a Function?
Every function is a relation, but not every relation is a function! Watch this video to learn how to tell which relations are functions and which are not.
-
How Do You Solve a Word Problem Using a System of Inequalities?
Math can sneak up in all sorts of places, so it's important to be prepared! Follow this tutorial to see a real world math problem involving a system of inequalities!
-
How Do You Solve a System of Equations Using Substitution if One Equation is a Quadratic?
Substitution is a great way to solve a system of equations! In this tutorial, you'll see how the substitution method is used to solve a system of equations involving both a linear and a quadratic equation!
-
How Do You Solve a System of Equations by Graphing if One Equation is a Quadratic?
Solving a system containing a quadratic equation by graphing is similar to solving a system of linear equations. In both cases, points of intersection play a key role. Watch the tutorial to find out more!
-
How Do You Solve a System of Equations by Graphing?
There are many different ways to solve a system of linear equations. In this tutorial, you'll see how to solve a system of linear equations by graphing both lines and finding their intersection. Take a look!
-
How Do You Solve a System of Equations Using the Substitution Method?
There are many different ways to solve a system of linear equations. In this tutorial, you'll see how to solve a system of linear equations by substituting one equation into the other and solving for the variable. Then, see how to use that variable value to find the value of the other variable. Check it out!
-
How Do You Solve a System of Equations Using the Elimination by Multiplication Method?
There are many different ways to solve a system of linear equations. In this tutorial, you'll see how to solve such a system by combining the equations together in a way so that one of the variables is eliminated. Then, see how find the value of that variable and use it to find the value of the other variable. Take a look!
-
How Do You Solve a System of Inequalities by Graphing?
There are many different ways to solve a system of inequalities. In this tutorial, you'll see how to solve such a system by graphing both inequalities and finding their intersection. Check it out!
-
How Can You Tell When a System of Equations Has Infinitely Many Solutions?
A system of linear equations can have one solution, no solution, or infinitely many solutions. That's right, infinitely many solutions! Watch this tutorial to find out how to identify systems that have infinitely many solutions.
-
How Do You Solve a Quadratic Equation with Two Solutions by Graphing?
One of the many ways you can solve a quadratic equation is by graphing it and seeing where it crosses the x-axis. Follow along as this tutorial shows you how to graph a quadratic equation to find the solution. Check it out!
-
How Do You Solve a Quadratic Equation by Factoring?
One of the many ways you can solve a quadratic equation is by factoring it. In this tutorial, you'll see how to factor a quadratic equation using the guess and check method of factoring. Then, use the zero product property to find the solution!
-
How Do You Solve a Quadratic Equation by Using the Quadratic Formula?
One of the many ways you can solve a quadratic equation is by using the quadratic formula. The quadratic formula is usually chosen when the other methods won't work or are difficult to use. In this tutorial, see how to solve a quadratic equation using the quadratic formula!
-
How Do You Solve a Quadratic Equation by Completing the Square?
One of the many ways you can solve a quadratic equation is by completing the square. In this method, you want to turn one side of the equation into a perfect square trinomial. This tutorial takes you through the steps of solving a quadratic equation by completing the square. Check it out!
-
How Do You Graph a Quadratic Function?
When you're trying to graph a quadratic equation, making a table of values can be really helpful. Before you make a table, first find the vertex of the quadratic equation. That way, you can pick values on either side to see what the graph does on either side of the vertex. Watch this tutorial to see how you can graph a quadratic equation!
-
How Do You Determine if a Graph Represents a Linear, Exponential, or Quadratic Function?
Graphs come in all sorts of shapes and sizes. In algebra, there are 3 basic types of graphs you'll see most often: linear, quadratic, and exponential. Check out this tutorial and learn how to determine is a graph represents a linear, quadratic, or exponential function!
-
What is a Quadratic Function?
You can't go through algebra without seeing quadratic functions. The graphs of quadratic functions are parabolas; they tend to look like a smile or a frown. In this tutorial, get introduced to quadratic functions, look at their graphs, and see some examples of quadratic functions!
-
What is the Discriminant?
In a quadratic equation, the discriminant helps tell you the number of real solutions to a quadratic equation. The expression used to find the discriminant is the expression located under the radical in the quadratic formula! In this tutorial, get introduced to the discriminant of a quadratic equation!
-
How Do You Simplify Radicals Using the Product Property?
Want to simplify a radical whose radicand is not a perfect square? No sweat! Check out this tutorial and see how to write that radicand as its prime factorization. Then, rewrite any duplicate factors using exponents, break up the radical using the product property of square roots, and simplify. To see this process step-by-step, watch this tutorial!
-
How Do You Multiply Radical Expressions Using FOIL?
Remember using FOIL to multiply binomials when you studied quadratics? It's back, this time with radicals. Combine what you know about multiplying radical expressions with FOIL and you can handle these products!
-
How Do You Add Radicals with Like Radicands?
Adding radicals isn't too difficult. As long as they have like radicands, you can just treat them as if they were variables and combine like ones together! This tutorial takes you through the steps of adding radicals with like radicands. Take a look!
-
How Do You Solve a Radical Equation?
Want some practice solving radical equations? Check out this tutorial! You'll see the steps you need to take in order to solve a radical equation and check your answer!
-
How Do You Solve a Radical Equation with a Binomial in the Radicand?
Want some practice solving radical equations? Check out this tutorial! You'll see the steps you need to take in order to solve a radical equation and check your answer!
-
How Do You Solve a Radical Equation with an Extraneous Solution?
When solving a radical equation, you may get an extraneous solution. Extraneous solutions aren't true solutions because they don't satisfy the original equation. Watch this tutorial to learn how to identify extraneous solutions.
-
How Do You Graph a Square Root Function Using a Table?
Making a table of values is a useful way to graph a square root function. Just remember to choose x-values for which the function is defined! Watch the tutorial to find out more.
-
What-Does-the-Value-of-'a'-Do-in-the-Function-f(x)=a%u221A(x)
When the parent square root function is multiplied by a constant, what happens to the function's graph? Follow along with the tutorial to investigate this question.
-
What Does the Constant 'k' Do in the Function f(x)=[square root of](x)+k?
When you're learning about translating square root functions, learning about vertical translations is a MUST! Check out this tutorial and see what it takes to translate a square root function vertically.
-
What Does the Parent Function Graph of a Square Root Function Look Like?
The square root parent function is the most basic member of the family of square root functions. How can you graph the parent function, and what does the graph look like? This tutorial answers these questions.
-
What's the Inverse Variation or Indirect Proportionality Formula?
Ever heard of two things being inversely proportional? Well, a good example is speed and time. The bigger your speed, the less time it takes to get to where you are going. So when one variable is big, the other is small, and that's the idea of inverse proportionality. But you can express inverse proportionality using equations, and that's an important thing to do in algebra. See how to do that in the tutorial!
-
How Do You Use the Formula for Inverse Variation to Write an Equation?
If two things are inversely proportional, you can bet that you'll need to use the formula for inverse variation to solve! In this tutorial, you'll see how to use the formula for inverse variation to find the constant of inverse variation and then solve for your answer.
-
How Do You Solve an AND Absolute Value Inequality and Graph It On a Number Line?
Trying to solve an absolute value inequality? No sweat! This tutorial will take you through the process of solving the inequality. Then you'll see how to write the answer in set builder notation and graph it on a number line. You'll see it all in this tutorial!
-
How Do You Factor a Polynomial Using the A-C Method?
Factoring trinomials can by tricky, but this tutorial can help! See how to use the A-C method to factor a trinomial into the product of two binomials. Then, use the FOIL method to multiply the two binomial back together to check your answer.
-
How Do You Factor a Polynomial Using Sum of Cubes?
Factoring a binomial involving addition? Can you rewrite each term as a cubed expression? Then you have a sum of cubes problem! Learn how to identify and factor a sum of cubes problem by watching this tutorial.
-
How Do You Find the Degree of a Polynomial?
Terms and polynomials can't run a fever, but they do have degrees! This tutorial will tell you all about the degree of a term and of a polynomial and will show you how to find it!
-
What is the Standard Form of a Quadratic?
Got a quadratic polynomial? Want to put it in standard form? Watch this tutorial to learn the steps it takes to make sure a quadratic polynomial is in standard form!
-
How Do You Add Two Rational Expressions with Different Denominators?
Adding rational expressions together? Don't have common denominators? No problem! Find the least common denominator (LCD) and change each rational expression into an equivalent expression with that LCD. Once you have common denominators, you're ready to add and simplify! Watch it all in this tutorial!
-
How Do You Find the Least Common Denominator of Two Rational Expressions?
When adding or subtracting rational expressions, you need have common denominators just like any other fraction. If you don't have common denominators, then you'll need to find the least common denominator (LCD) and use it to get those denominators to be the same. Learn how to find the LCD of two rational expressions by watching this tutorial!
-
How Do You Multiply Two Rational Expressions?
Multiplying together two rational expression isn't so hard, especially if you know the proper steps! This tutorial will take you through all the steps necessary to multiply together two rational expressions and then simplify the product to get the answer. Check it out!
-
How Do You Do Long Division With Polynomials?
Dividing polynomials? Use long division! Follow along as this tutorial shows you how to perform long division with polynomial. Check it out!
-
What is Domain?
Did you know that a relation has a domain? The domain of a relation is the set of the first coordinates from the ordered pairs. This tutorial defines the domain of a relation!
-
What's the Inverse of a Relation?
Did you know there's something called the inverse of a relation? Watch this tutorial to learn the definition for the inverse of a relation and to see an example!
-
What's a Function?
You can't go through algebra without learning about functions. This tutorial shows you a great approach to thinking about functions! Learn the definition of a function and see the different ways functions can be represented. Take a look!
-
How Do You Graph an Absolute Value Inequality on the Coordinate Plane?
Graphing an absolute value inequality in two variables is similar to graphing a linear inequality in two variables. In both cases you first graph an equation to create a boundary for the graph of the inequality, and then shade one side of the boundary. Watch the tutorial to learn more!
-
How Do You Write an Absolute Value Inequality from a Graph?
If you start with the graph of an absolute value inequality, can you determine the inequality used to generate the graph? The answer is yes! Follow along with the tutorial to see how this works.
-
How Do You Translate a Function?
Think about sliding a penny on a table. All you're doing is moving the penny to a new location on the table. That's basically all that's happening when you translate a function! When you translate a function, you're just sliding it to a new location on the coordinate plane!
-
How Do You Graph a Translation of a Function?
A great way to better understand how to translate a function is to practice! This tutorial takes you through the steps of graphing a function that's been translated up and to the right.
-
What is a One-to-One Function?
What is a one-to-one function? What qualities make a function one-to-one? This tutorial is a great introduction and explanation for one-to-one functions!
-
What is a Regression Line?
Scatterplots of data on the coordinate plane sometimes reveal patterns. If the data appears to be roughly linear. A line drawn through the middle of the data, or regression line, can be used to make predictions about the data. Check out the video to learn more about regression lines!
-
What is Linear Regression?
Sometimes Real-world data follows a linear pattern. A linear regression is a the equation for a linear function that most closely follows the given data. Watch the tutorial to learn more about modeling data with linear functions.
-
How Do You Solve a System of Equations in Three Variables Using Elimination?
The elimination method can be extended from solving a system of equations with two variables to solving a system with three variables. Watch the tutorial to find out how!
-
How Do You Solve a System of Equations in Three Variables Using Substitution?
The substitution method can be extended from solving a system of equations with two variables to solving a system with three variables. Follow along with the tutorial to see how this is done.
-
How Do You Solve an Optimization Word Problem?
Optimization problems are used everyday to help businesses figure out how much of their products they need to sell in order to make a profit. Follow along with this tutorial to see a real world problem involving optimization!
-
What is Linear Programming?
If you want to solve an optimization problem, you can use linear programming to help! This tutorial introduces linear programming and the different pieces of this method.
-
How Do You Add Matrices?
Adding matrices is easier than you might think! Just find the corresponding positions in each matrix and add the elements in them! This tutorial can show you the entire process step-by-step.
-
How Do You Multiply a Matrix by a Scalar?
To multiply a matrix by a scalar, just multiply each element in the matrix by the scalar! To see the entire process, check out this tutorial!
-
How Do You Multiply Two 2x2 Matrices?
Multiplying matrices isn't as simple as multiplying real numbers, but it's not too hard once you understand the procedure. Watch this tutorial to see how multiplication works for 2 x 2 matrices.
-
How Do You Find Values For x and y to Make Two Matrices Equal?
Two matrices with the same dimensions are equal if the elements in corresponding positions are equal. Watch this tutorial to see how the definition of matrix equality can be used to find unknown values in matrices.
-
How Do You Find the Determinant of a 2x2 Matrix?
Determining the determinant of a matrix can be fun, especially when you know the right steps! This tutorial provides a great example of finding the determinant of a 2x2 matrix.
-
How Do You Find the Inverse of a 2x2 Matrix?
When you multiply a matrix and its inverse together, you get the identity matrix! Follow along with this tutorial to practice finding the inverse of a 2x2 matrix.
-
What is a Matrix?
Matrices can help solve all sorts of problems! This tutorial explains what a matrix is and how to find the dimensions of a matrix.
-
What Is an Element of a Matrix?
A matrix is a rectangular array of numbers called elements. Watch this tutorial to find out more about the elements of a matrix.
-
What is a Coefficient Matrix?
You can solve a system of a equations using matrices! In order to do that, you need to create a coefficient matrix. This tutorial introduces this type of matrix and shows you how to make one!
-
How Do You Add Complex Numbers?
If you want to add complex numbers together, first regroup them so that like terms are next to one another. Then, add the like terms together, and you have your answer! To see an example, check out this tutorial.
-
How Do You Solve a Quadratic Inequality by Graphing?
You can solve a quadratic inequality by graphing! Follow along with this tutorial to see how to graph a quadratic inequality and use that graph to find the solution!
-
How Do You Write an Equation For a Quadratic if You Have Three Points?
Three points determine a parabola, so given three points you can write the parabola's equation. This tutorial will show you how!
-
How Do You Convert a Quadratic from Standard Form to Vertex Form by Completing the Square?
The vertex form of a quadratic equation can help you quickly identify the vertex of that quadratic. Follow along with this tutorial to see how to use the completing the square method to change a quadratic equation from standard form to vertex form!
-
What is the Imaginary Unit i?
Every tried to take the square root of a negative number? You'll need the imaginary unit 'i' to write the answer. This tutorial introduces you to this useful imaginary unit.
-
What is a Quadratic Inequality?
A quadratic inequality is just like a quadratic equation, except instead of an equal sign there's an inequality! Check out this tutorial to see the characteristics of a quadratic inequality and get some practice identifying them.
-
What is Vertex Form of a Quadratic Equation?
What does the vertex form of a quadratic equation look like, and what does it tell you about the equation's graph? Watch this tutorial to unlock the secrets of the vertex form!
-
How Do You Solve a Polynomial Equation by Rewriting it in Quadratic Form?
Some polynomial equations that look tough can be rewritten in a quadratic form and then solved by methods that you have used before. This tutorial will show you how!
-
How Do You Find All the Rational Zeros of a Polynomial Function?
Polynomial functions with integer coefficients may have rational roots. The Rational Root Theorem lets you determine the possible candidates quickly and easily! Watch the video to learn more.
-
How Do You Find All the Zeros of a Polynomial Function with Imaginary Zeros?
Not all zeros of a polynomial function are necessarily rational. Using synthetic division to test possible zeros can lead to the bonus of a factoring of the polynomial. From there you may be able to use methods for quadratic equations to find those imaginary roots. If they exist!
-
What is the Fundamental Theorem of Algebra?
Does every polynomial function have a solution? The answer can be found through the Fundamental Theorem of Algebra! This tutorial introduces you to the theorem and explains how its meaning.
-
What is a Polynomial Function?
Polynomial functions all have the same general form, but come in many varieties. You can categorize them based on their degree and the number of terms they have. Check out this video to learn more!
-
What are the Roots, or Zeros of a Polynomial Function?
Knowing the roots, or zeros, of a function can help you graph it. The degree of a polynomial function determines the number of roots it has. Watch the video to learn more!
-
What is Synthetic Division?
Tired of all of those variables in your polynomial division problems? Throw them out with synthetic division! Watch the video to learn how.
-
What is the Rational Zero Theorem?
This is a handy method for finding the rational roots, or zeros, of a polynomial function. You can use the coefficient of the highest-degree term and the value of the constant to determine all of the possible rational roots or zeros. Watch the video to learn more.
-
What is the Factor Theorem?
Trying to figure out if a given binomial is a factor of a certain polynomial? This tutorial can help you find the answer! Follow along to learn about the Factor Theorem and how it can be used to find the factors and zeros of a polynomial.
-
How Do You Find the Cube Root of a Perfect Cube?
To find the cube root of a number, start by breaking that number into its prime factorization. Rewrite those factors using exponents and break up the radicals using the Product Property of Radicals. Simplify and you're done! Watch this tutorial to see the entire process step-by-step.
-
How Do You Find the Cube Root of a Perfect Cube with Variables?
Simplifying cube root expressions that contain variables is pretty similar to dealing with numerical cube root expressions. Use the laws of exponents to rewrite variables in the radicand so that they can be simplified. Check out the video to learn how!
-
How Do You Find the Sum of Two Functions?
Adding functions is easier than you might think! Follow along with this tutorial to learn how to add two functions together.
-
How Do You Simplify a Radical When the Radicand is Not a Perfect nth Power?
Sometimes when you simplify radical expressions there are leftovers. Follow the tutorial to see how to handle them.
-
How Do You Find the Inverse of a Linear Function?
The steps for finding the inverse of a linear function are a lot like those for solving a linear equation. In both cases you need to isolate a variable in an equation. Watch this tutorial to learn more about finding inverses of linear functions!
-
How Do You Graph a Cube Root Function Using a Table?
You can make a table of values to graph a cube root function. The graph should generally resemble the parent cube root function. Follow this tutorial to learn more.
-
What are Compositions of Functions?
A composition of two functions uses the output of one function as the input of the other. Watch this tutorial to learn more about function composition!
-
What are Rational Exponents?
You can rewrite an expression with a rational exponent a few different ways. This can come in handy when your solving a problem involving rational exponents. This tutorial shows you how it works! You can even practice with examples!
-
What are the Properties of Rational Exponents?
The Properties of Rational Exponents follow from the definition of exponent. They are the same properties you worked with previously, when the exponents were integers. Now you can apply these properties and convert between exponential and radical forms. See the video to learn more.
-
How Do You Convert From Exponential Form to Logarithmic Form?
Having a problem in exponential form is great, but can you change it to logarithmic form? This tutorial shows you that process step-by-step!
-
How Do You Convert From Exponential Form to Natural Logarithmic Form?
Converting from exponential form to natural logarithmic form is easier than you might think! Follow along with this tutorial to see how to perform this conversion.
-
What Does the Constant 'k' Do to the Graph of f(x)=log(x)+k?
Translating a logarithmic function vertically can be fun, especially when you know how it's done! This tutorial shows what it takes to shift a logarithmic function up and down!
-
What Does the Value of 'a' Do to the Graph of f(x)=a%u2022log(x)?
Multiplying a logarithmic function by a constant changes the function's graph in a certain way. Check out this video to see how!
-
How Do You Graph the Natural Base Exponential Function?
Want to graph a natural base exponential function? Make a table of points! Then plot the points, connect them, and you have your graph! Follow along with this tutorial to see the entire process step-by-step.
-
How Do You Expand a Logarithmic Expression Using Properties of Logarithms?
The properties of logarithms are useful for rewriting logarithmic expressions. Watch the tutorial to learn how these properties can be used to expand a logarithmic expression.
-
How Do You Solve a Logarithmic Equation by Exponentiating?
Equations involving logarithms don't have to be scary. Just get rid of the logarithm by exponentiating and solve like any other equation! This tutorial shows you all the steps.
-
How Do You Solve an Exponential Equation Using Logarithms?
If you can't rewrite each side of an exponential equation using the same base, use logarithms to help you solve the equation. Watch this video and find out how!
-
What is a Logarithm?
Logarithms can be tricky, but they become a whole lot easier if you understand how they're related to exponents. Follow along with the tutorial to learn about this relationship.
-
What is a Natural Logarithm?
A natural logarithm is a logarithm that has a special base. In this tutorial, you'll be introduced to natural logarithms!
-
What is a Natural Logarithmic Function?
The natural logarithmic function is a particularly important member of the family of logarithmic functions. Watch the tutorial to find out more about this special function!
-
What is the Natural Base Exponential Function?
The natural base exponential function is actually a function that's shorter than its name! This tutorial introduces you to this special function and shows you what it looks like.
-
What is the Product Property of Logarithms?
If you want to add together logarithms with the same base, the Product Property of Logarithms can help! In this tutorial, you'll learn about this helpful property and see how it can be used to quickly add logarithms with the same base.
-
How Do You Graph a Rational Function by Finding its Asymptotes and Zeros?
In a rational function, the denominator of the rational expression holds the key to the location of the vertical asymptotes. The relationship between degrees of the numerator and denominator determine the nature of the horizontal asymptotes. Check out the tutorial to learn more!
-
How Do You Use the Equation for a Rational Function to Find Its Horizontal Asymptotes?
Rational functions behave predictably as they head off to infinity. Follow this tutorial to learn more about their asymptotic behavior!
-
What is the Standard Form of the Equation of a Parabola With a Vertex (h,k)?
Given the vertex and one other point on a parabola, you can write the equation of the parabola in standard form. Watch this tutorial to find out how!
-
What is a Parabola?
A parabola is much more than just the graph of a quadratic. This tutorial shows you various definitions of a parabola and even shows you horizontal parabolas! Take a look!
-
What is Conditional Probability?
If you're learning about probability, conditional probability is bound to come up. This tutorial explains conditional probability and shows you how to find it!
-
How Do You Write and Use a Prediction Equation?
Scatter plots are a great way to see data visually. They can also help you predict values! Follow along as this tutorial shows you how to draw a line of fit on a scatter plot and find the equation of that line in order to make a prediction based on the data already given!
-
How Do You Find Volumes of Similar Solids?
There's a way to find out the ratio of the volumes of similar solids — but it's not as simple as comparing the sides. Watch this tutorial to find out how!
-
What is a Solid?
Understanding solids is a building block for finding their lateral area, surface area, and volume. In this tutorial, you'll see examples of solids and learn their different parts. Take a look!
-
What is the Relationship Between the Surface Areas of Similar Solids?
If you have similar solids, there's a ratio that relates their surface areas. This tutorial uses similar prisms to help you find the ratio rule of the surface areas of any similar solids!
-
How Do You Add Polynomials Vertically?
Want to see how to add two polynomials vertically? Then this tutorial is for you! In this tutorial, you'll see the steps you need to follow in order to add polynomials vertically.
-
How Do You Graph a Cubic Function Using a Table?
Making a tables to graph a cubic functions is a great way to help understand their nature. Use some friendly x-values, find their corresponding y-values, and graph!
-
What is a Cubic Function?
Cubic functions are just one type of function you’ll see in math. This tutorial introduces you to cubic functions, shows you some examples and graphs, and explains the parent function of cubic functions. Check out this tutorial to learn about cubic functions!

























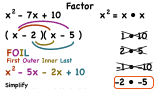


















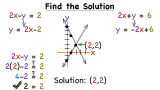








































+k?](https://cdn.virtualnerd.com/thumbnails/Alg1_13_01_0025-diagram_thumb.png)
+k?](https://cdn.virtualnerd.com/thumbnails/Alg1_13_01_0025-video_thumb.png)