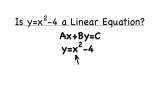Functions
More Specific Topics in Functions
Popular Tutorials in Functions
-
What's a Function?
Function rules are like instructions on how to change input values into their respective output values. In this tutorial, see how to write a function rule for a given relation. Check it out!
-
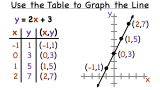
How Do You Graph a Linear Equation From a Table?
A table of values for a linear equation can be very helpful, but a graph of the equation can be even better! In this tutorial, you'll see how to use a table of values to graph a linear equation!
-
How is a Function Defined?
You can't go through algebra without learning about functions. This tutorial shows you the definition of a function and gives you an example of a function. Take a look!
-
How Do You Write an Equation of a Line in Slope-Intercept Form If You Have Two Points?
Trying to write an equation in slope-intercept form? Have two points on your line? You'll need to find your slope and y-intercept. Watch this tutorial and see what needs to be done to write an equation in slope-intercept form!
-
How Do You Write an Equation of a Line in Slope-Intercept Form from a Word Problem?
Word problems are a great way to see math in the real world! In this tutorial, you'll see how write an equation in slope-intercept form that represents the information given in the word problem. To see how it's done, check out this tutorial!
-
What's Slope-Intercept Form of a Linear Equation?
When you're learning about linear equations, you're bound to run into the point-slope form of a line. This form is quite useful in creating an equation of a line if you're given the slope and a point on the line. Watch this tutorial, and learn about the point-slope form of a line!
-
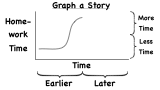
How Do You Make an Approximate Graph From a Word Problem?
Sometimes a word problem describes a situation that can be better understood if it were graphed. This tutorial gives an example of one such word problem. Check it out!
-
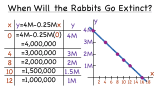
How Do You Use the Graph of a Linear Equation to Solve a Word Problem?
Word problems are a great way to see math in the real world! In this tutorial, see how to figure out how long it will take for a rabbit population to go extinct. You'll also see how to set up a table and a graph to help find the answer!
-
How Can You Tell If You Have a Linear Equation?
Trying to figure out if an equation is a linear equation? Well, can you write it in standard form? If you can, then it's a linear equation. See this process in action by watching this tutorial!
-
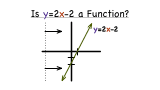
How Do You Figure Out If a Relation is a Function?
How do you figure out if a relation is a function? You could set up the relation as a table of ordered pairs. Then, test to see if each element in the domain is matched with exactly one element in the range. If so, you have a function! Watch this tutorial to see how you can determine if a relation is a function.
-
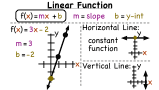
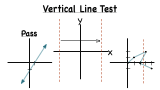
How Do You Use the Vertical Line Test to Figure Out if a Graph is a Function?
Trying to figure out if an equation is a function? Graph it and perform the vertical line test. If it passes, then it's a function! Get some practice by watching this tutorial!
-
What's a Function?
You can't go through algebra without learning about functions. This tutorial shows you a great approach to thinking about functions! Learn the definition of a function and see the different ways functions can be represented. Take a look!
-
What's the Vertical Line Test?
Even graphs need to worry about tests! Using the vertical line test, you can figure out if a graph is a function or not. Watch this tutorial and learn about the vertical line test. Then, put your graphs to the test!
-
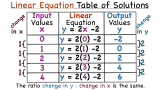
How Do You Make a Table of Values for a Linear Equation?
To graph a linear equation, you could make a table of values to plot, but first you'll need to know how to make the table. Take a look at this tutorial! You'll see how to set up a table, choose appropriate x-values, plug those values into the equation, and simplify to get the respective y-values. This tutorial shows you how to set up a table of values for a linear equation!
-
How Do You Write the Equation of a Line in Slope-Intercept Form If You Have a Graph?
Working with the graph of a line? Trying to find the equation for that graph? Just pick two points on the line and use them to find the equation. This tutorial shows you how to take two points on the graph of a line and use them to find the slope-intercept form of the line!
-
How Do You Write the Equation of a Line in Slope-Intercept Form If You Have a Table?
Looking at a table of values that represents a linear equation? Want to find that equation? Then check out this tutorial! You'll see how to use values from a table to find the slope-intercept form of the line described in the table.
-
What is a Linear Equation?
If you're learning about graphs, you're bound to see a bunch of linear equations, so it's a good idea to understand what makes an equation a linear equation. This tutorial explains linear equations and shows you the difference between equations that are linear and ones that are not. Check it out!