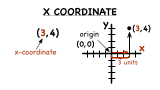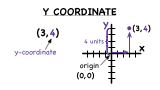What's the Formula for Slope?
Note:
When you're dealing with linear equations, you may be asked to find the slope of a line. That's when knowing the slope formula really comes in handy! Learn the formula to find the slope of a line by watching this tutorial.