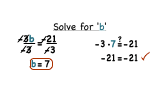How Do You Use the Formula for Inverse Variation to Write an Equation?
Note:
If two things are inversely proportional, you can bet that you'll need to use the formula for inverse variation to solve! In this tutorial, you'll see how to use the formula for inverse variation to find the constant of inverse variation and then solve for your answer.
Keywords:
- problem
- indirect variation
- variation
- indirect
- indirect proportionality
- proportional
- constant of variation
- find constant of variation
- evaluate
- apply proportion
- inverse
- inverse proportionality
- inverse variation
Background Tutorials
-
Evaluating Expressions
-
What is a Variable?
You can't do algebra without working with variables, but variables can be confusing. If you've ever wondered what variables are, then this tutorial is for you!
-
-
Working with Inverse Variation
-
What's the Inverse Variation or Indirect Proportionality Formula?
Ever heard of two things being inversely proportional? Well, a good example is speed and time. The bigger your speed, the less time it takes to get to where you are going. So when one variable is big, the other is small, and that's the idea of inverse proportionality. But you can express inverse proportionality using equations, and that's an important thing to do in algebra. See how to do that in the tutorial!
-
-
Simplifying Expressions
-
What is a Constant?
Constants are parts of algebraic expressions that don't change. Check out this tutorial to see exactly what a constant looks like and why it doesn't change.
-
-
Solving Equations by Dividing
-
How Do You Solve an Equation Using Division?
Solving an equation for a variable? Perform the order of operations in reverse! Check it out in this tutorial.
-
Further Exploration
-
Working with Inverse Variation
-
How Do You Solve a Word Problem Using Inverse Variation?
If two things are inversely proportional, you can bet that you'll need to use the formula for inverse variation to solve! In this word problem, you'll see how to use the formula for inverse variation to find the constant of inverse variation and then solve for your answer.
-
What's the Inverse Variation or Indirect Proportionality Formula?
Ever heard of two things being inversely proportional? Well, a good example is speed and time. The bigger your speed, the less time it takes to get to where you are going. So when one variable is big, the other is small, and that's the idea of inverse proportionality. But you can express inverse proportionality using equations, and that's an important thing to do in algebra. See how to do that in the tutorial!
-